미로탈출

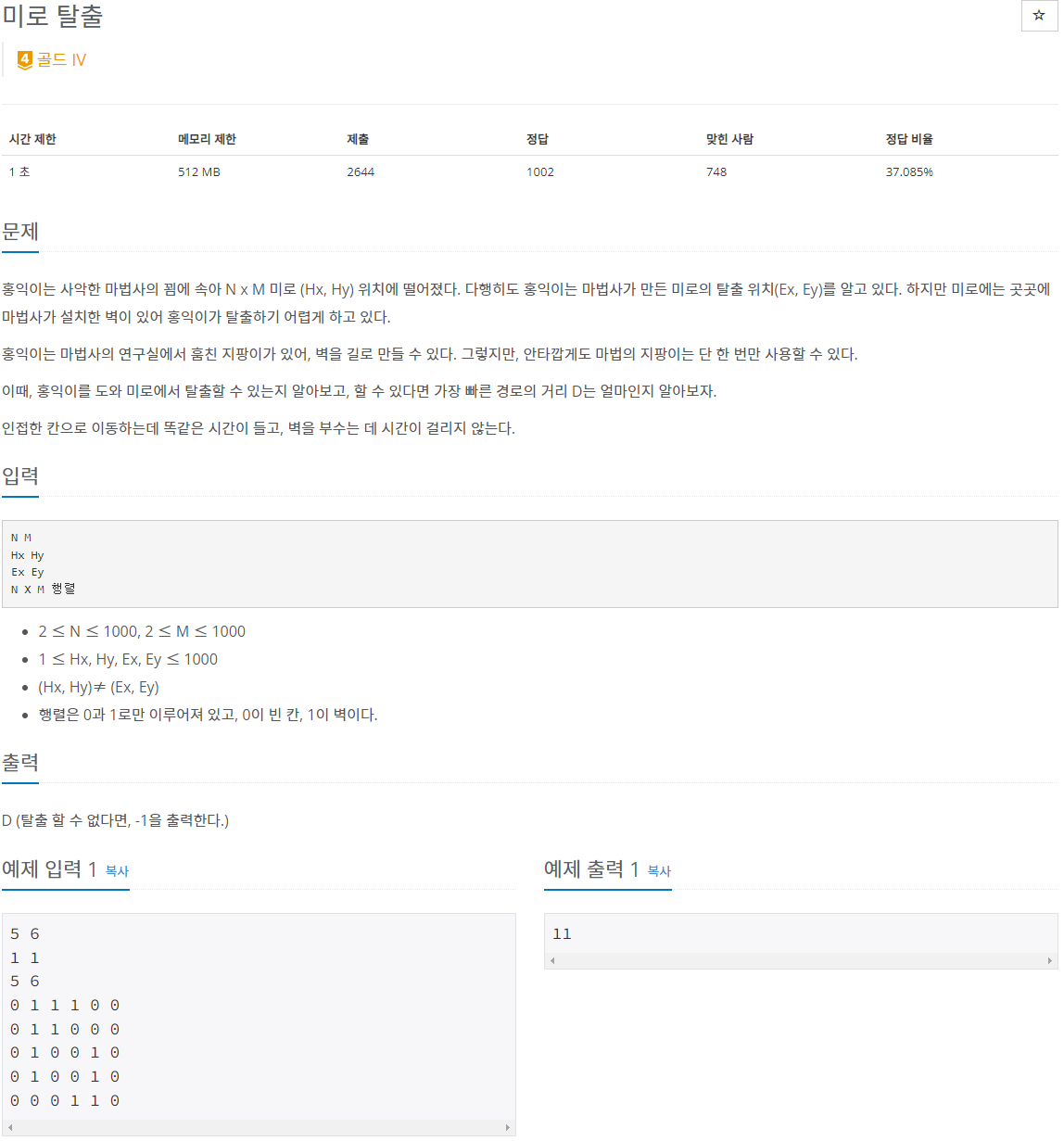
📍 문제 설명

 

💡 접근

처음에는 지팡의 갯수중에 1개를 뽑는 조합 문제라고 생각했는데, 범위가 작은 편이 아니었다.

방문체크하는 배열에 지팡이 사용 여부도 추가한 3차원 배열을 이용했다.

이렇게 하면 지팡이 사용하지 않았을 때 / 한 지점에 대해 지팡이를 사용하여 길을 뚫은 모든 경우에 대한 최단 경로가 나온다.

 

👩‍💻 코드

import java.util.*;

public class Main {
    static int n, m, answer, cnt, max, min;
    static int Hx, Hy, Ex, Ey;
    static int[][] board, clone;
    static int[][] dis;
    static boolean[][] visited,successRoute;
    static int[] parent = new int[100001];
    static int[] ch,pm, combi, graph;
    static boolean flag = false;
    static int[] dx = {-1,1,0,0};
    static int[] dy = {0,0,-1,1};
    public static void main(String[] args) {
        Main T = new Main();
        Scanner kb = new Scanner(System.in);

        n = kb.nextInt();
        m = kb.nextInt();
        Hx = kb.nextInt();
        Hy = kb.nextInt();
        Ex = kb.nextInt();
        Ey = kb.nextInt();
        board = new int[n+1][m+1];
        clone = new int[n+1][m+1];
        for(int i = 1; i <= n; i++) {
            for(int j = 1; j <= m; j++) {
                board[i][j] = kb.nextInt();
            }
        }
        T.solution();
    }

    private void solution() {
        Queue<Point> q = new LinkedList<>();
        boolean visit[][][] = new boolean[n+1][m+1][2];
        //출발 지점, cnt는 지팡이를 사용한 횟수, 이동 거리
        q.offer(new Point( Hx, Hy, 0, 0 ));
        //지팡이 사용유무에 따른 좌표 방문 여부
        visit[Hx][Hy][0] = true;

        while(!q.isEmpty()) {
            System.out.println(q);
            Point p = q.poll();

            //도착지점에 도달했으면 이 거리가 최단거리이다.
            if(p.x == Ex && p.y == Ey) {
                System.out.println(p.dis);
                return;
            }
            for(int i = 0; i < 4; i++) {
                int nx = p.x + dx[i];
                int ny = p.y + dy[i];

                if(nx<1 || ny<1 || nx>n || ny>m || visit[nx][ny][p.cnt]) continue;

                //다음 지점 벽인데 지팡이 사용안했으면 해당 지점을 방문할 수 있다.
                if(board[nx][ny] == 1 && p.cnt == 0) {
                    visit[nx][ny][p.cnt] = true;
                    q.add(new Point(nx, ny, 1, p.dis+1));
                }
                //길이면 그냥 이동한다.
                else if(board[nx][ny] == 0) {
                    visit[nx][ny][p.cnt] = true;
                    q.add(new Point(nx, ny, p.cnt, p.dis+1));
                }
            }
        }
        System.out.println(-1);
    }

    private class Point {
        private int x;
        private int y;
        private int cnt;
        private int dis;

        public Point(int x, int y, int cnt, int dis) {
            this.x = x;
            this.y = y;
            this.cnt = cnt;
            this.dis = dis;
        }

        @Override
        public String toString() {
            return "Point{" +
                    "x=" + x +
                    ", y=" + y +
                    ", cnt=" + cnt +
                    ", dis=" + dis +
                    '}';
        }
    }
}