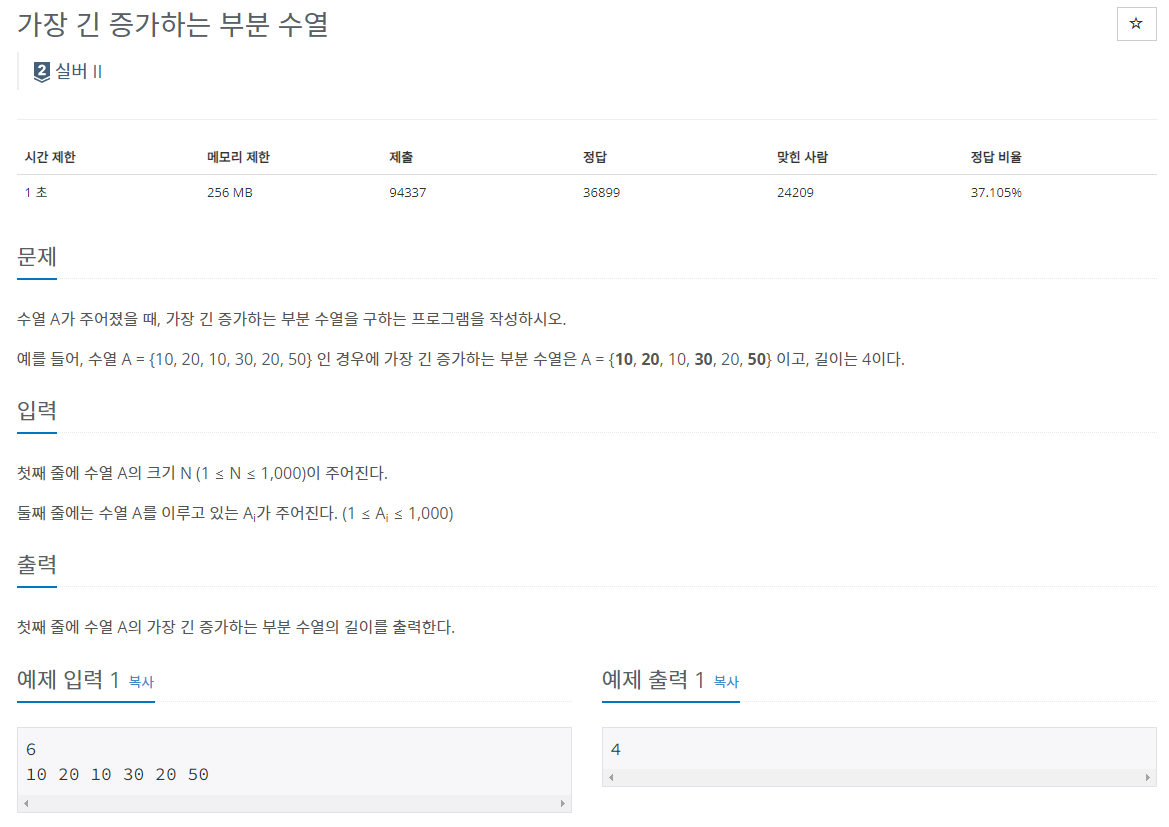
📍 문제 설명
💡 접근
인프런 강의에서 배웠던 최대부분증가수열(LIS) 문제다.
dp[n]을 n번째 인덱스를 마지막 항으로 하는 최대 증가 부분 수열로 둔다.
i = 1일 때 j = 0 탐색
j = 0 -> arr[0] < arr[1] && dp[0] > max 이므로 max = dp[0] = 1
dp[1] = 1 + 1 = 2
i = 2일 때 j = 1, 0 탐색
j = 1 -> 이전 항이 더 크다. dp[2] = 1
j = 0 -> 이전 항이랑 같다. dp[2] = 1
i = 3일 때 j = 2, 1, 0 탐색
j = 2 ->max = 1 dp[3] = 2
j = 1 ->max = 2 dp[3] = 3
j = 0 -> dp[0] < max dp[3] = 3
👩💻 코드
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static int n, m, answer;
static int[][] board;
static int[] arr, dp;
static boolean[][] visited;
static int[] dx = {-1,1,0,0};
static int[] dy = {0,0,-1,1};
static ArrayList<String> list = new ArrayList<>();
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) {
Scanner kb = new Scanner(System.in);
Main T = new Main();
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int n = kb.nextInt();
arr = new int[n];
for(int i = 0; i < n; i++) {
arr[i] = kb.nextInt();
}
//dp[n]은 n번째 인덱스를 마지막 항으로 하는 최대 증가 부분 수열
dp = new int[n];
dp[0] = 1;
for(int i = 1; i < n; i++) {
int max = 0;
//현재 항의 이전 항들을 탐색
for(int j = i-1; j >= 0; j--) {
//1. 이전 항이 현재 항 보다 더 작아야함
//2. 이전 항의 길이가 max 값보다 커야함
if(arr[j] < arr[i] && dp[j] > max) max = dp[j];
//
dp[i] = max + 1;
answer = Math.max(answer, dp[i]);
}
}
System.out.println(answer == 0 ? 1 : answer);
}
private void solution() {
}
}