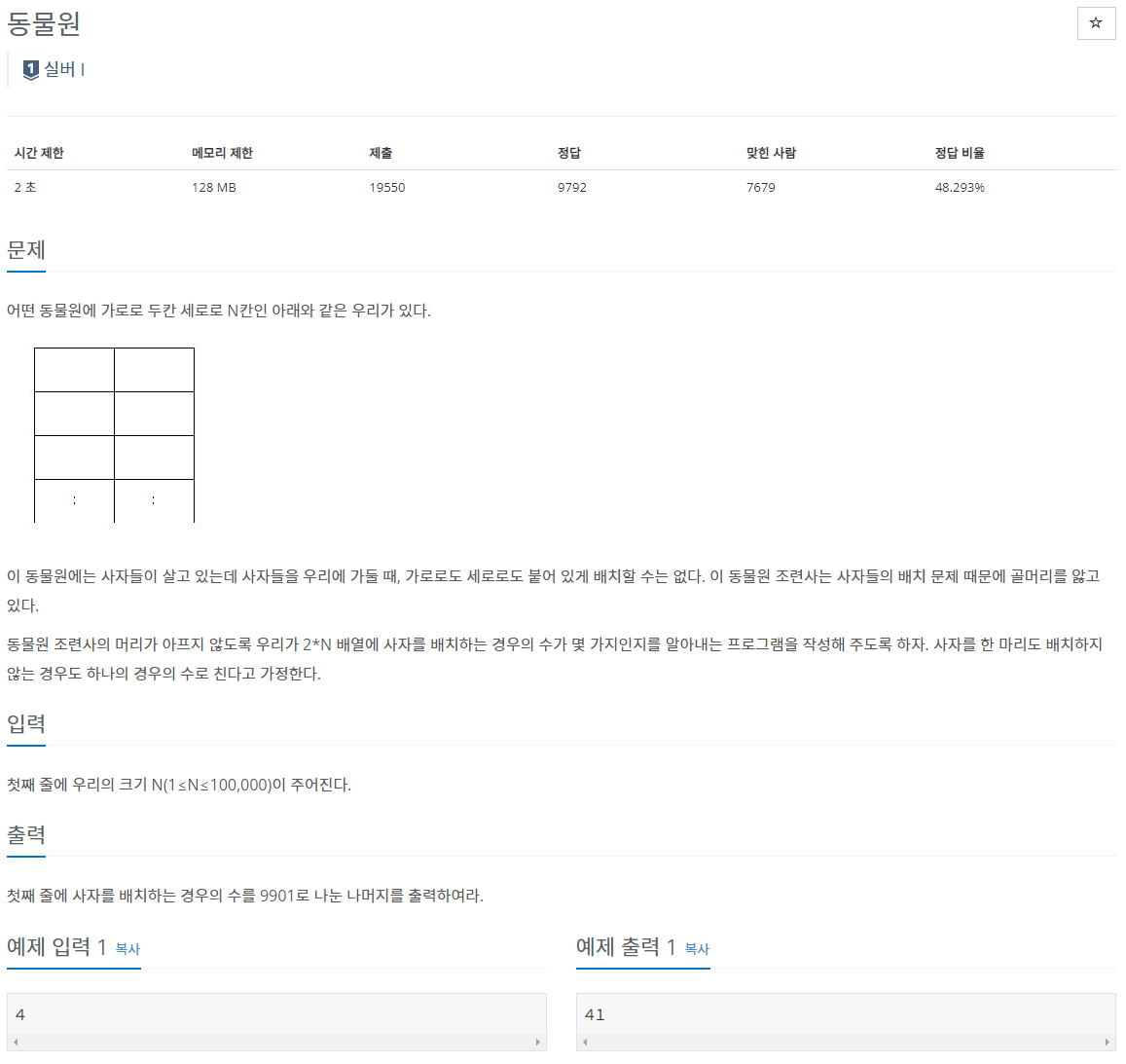
📍 문제 설명
💡 접근
2차원 배열을 이용한다. 위쪽 우리의 사자의 위치에 따라 경우의 수를 계산한다.
사자가 없거나 왼쪽에 사자가 있거나 오른쪽에 사자가 있거나 3가지 중에 하나이다.
사자가 없으면 어느 위치에도 구애 받지 않으므로 놓지 않거나/왼쪽에 놓거나/오른쪽에 놓거나가 된다.
사자가 왼쪽에 있으면 놓지 않거나/오른쪽에 놓거나가 된다.
사자가 오른쪽에 있으면 놓지 않거나/왼쪽에 놓거나가 된다.
👩💻 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.*;
public class Main {
static int n, m, answer = Integer.MAX_VALUE, max, k, min;
static int[][] board;
static long[][] arr, dp, t, p;
static boolean[][] visited;
static int[] dx = {-1,1,0,0};
static int[] dy = {0,0,-1,1};
static ArrayList<String> list = new ArrayList<>();
static StringBuilder sb = new StringBuilder();
public static void main(String[] args) throws IOException {
Scanner kb = new Scanner(System.in);
Main T = new Main();
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
n = kb.nextInt();
dp = new long[n+1][3];
T.solution();
}
private void solution() {
dp[1][0] = dp[1][1] = dp[1][2] = 1;
for(int i = 2; i <= n; i++) {
dp[i][0] = (dp[i-1][0] + dp[i-1][1] + dp[i-1][2]) % 9901;
dp[i][1] = (dp[i-1][0] + dp[i-1][2]) % 9901;
dp[i][2] = (dp[i-1][0] + dp[i-1][1]) % 9901;
}
long cnt = (dp[n][0] + dp[n][1] + dp[n][2]) % 9901;
System.out.println(cnt);
}
}